Contenu du cours
Ce cours s'inscrit dans la continuité de celui dispensé en première année et étend l'étude des fonctions d'une variable réelle à celles des fonctions à plusieurs variables.
Pour s'assurer de bien suivre ce cours, il sera important de maîtriser les notions de bases en algèbre linéaire comme le calcul vectoriel et matriciel, la détermination de valeurs propres ou encore quelques élements de géométries liés au produit scalaire.
Une première partie sera consacrée à l'étude de la continuité et de dérivabilité des fonctions de plusieurs variables sans pour autant fournir autant de résultats que ce qui ont été vus en première année.
Nous verrons également le fonctionnement du calcul d'intégrales dans un tel contexte.
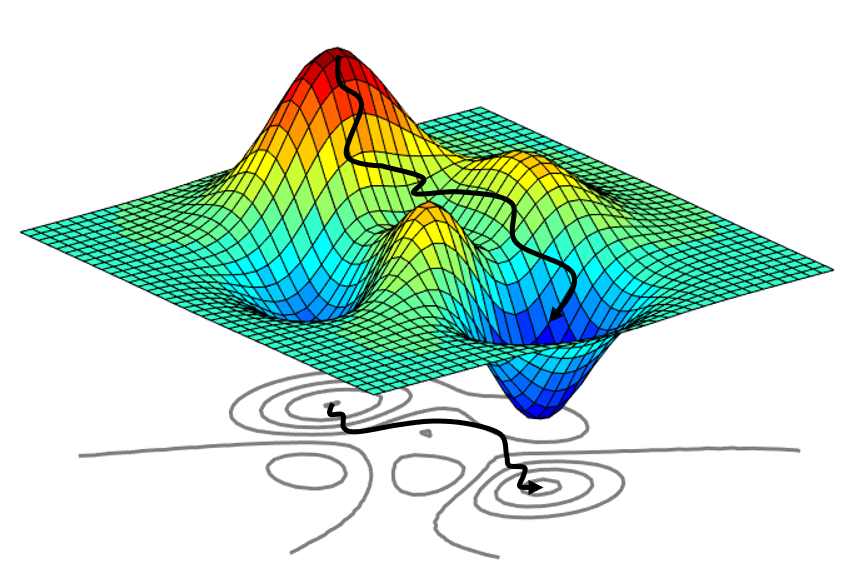
Après avoir revu les notions de convexité et la caractérisation de cette propriété pour de telles fonctions, nous souhaitons ensuite mobiliser ces connaissances pour mettre en oeuvre quelques algorithmes d'optimisation basés sur la descente de gradient afin de trouver le minimum d'une fonction de façon numérique.
Une fiche de TD est disponible pour vous permettre de vous entraîner. Une séance de TD sera également consacrée à une partie mise en pratique sous Python afin d'illustrer les résultats vus en cours.
Ressources cours
Le document ci-dessous est un polycopié du cours qui permet de reprendre le contenu des slides avec des explications supplémentaires ainsi que des "exercices" permettant de vérifier la bonne compréhension des notions.
Travaux Dirigés
Une fiche d'exercice qui permet de mettre en application les différentes notions vues en cours. Les exercices sont essentiellement calculatoires mais certains peuvent être plus abstraits. Il sera également possible d'illustrer certains résultats des exercices de cette fiche à l'aide de Python. Cela sera le cas pour les exercices qui concernent l'optimisation de fonctions.
Examens théoriques
Contient les examens et éventuellement les corrections des années précédentes.