La prétopologie : un outil de modélisation
De nombreux outils mathématiques permettent de modéliser les systèmes :
la théorie des graphes qui permet de modéliser des relations binaires
entre les éléments d'un ensemble, la topologie ou les espaces métriques
qui permettent de définir des notions de proximité pour analyser la
structure d'un ensemble, ... . Ces outils mathématiques sont parfaitement
adaptés à de nombreuses de situations. En revanche, dans certaines
applications spécifiques à certains secteurs comme celui des sciences
humaines et sociales, ces outils ont montré quelques limites, en
particulier pour appréhender des systèmes discrets où les éléments
sont des individus, des ensembles d'individus, des agents économiques, des
secteurs d'activités, ..., avec des relations complexes qui rendent
impossible la création d'une métrique ou d'un graphe, et dont il faut
suivre la dynamique qui reste rapidement bloquée dans des ouverts ou
fermés en topologie.
En appauvrissant les axiomes de la topologie, la prétopologie apporte un cadre conceptuel et opérationnel bien adapté à la modélisation des systèmes complexes comme ceux rencontrés en sciences humaines et sociales. Elle apporte ainsi des solutions effectives à la modélisation des problèmes où les relations entre les éléments étudiés sont non métriques et de nature très diverse.
Qu'est-ce qu'un espace prétopologique :
Soit E un ensemble non vide. Soit a(.) une application définie de P(E)
(l'ensemble des parties de E) dans P(E) vérifiant :
- a(∅) = ∅,
- ∀A ∈ P(E), A ⊂ a(A).
a(.) définit ainsi une structure prétopologique sur E. (E,a) est appelé espace prétopologique et a(A) l'adhérence de la partie A.
La prétopologie offre un cadre mathématique général qui généralise, entre autres, la topologie et la théorie des graphes, et apporte un ensemble d'outils et de propriétés mathématiques comme la connexité, la séparabilité, la continuité, la compacité, ... .
Structuration d'ensemble
Comme souvent en SHS, on étudie et on cherche à mieux comprendre l'organisation d'un ensemble d'individus (personnes physiques, entreprises, régions, ...) reliés entre eux par des relations quelconques, comme par exemple "est proche de", "est influent sur", "est indispensable à", "travaille avec", ... . L'objectif de ces études est d'extraire une structuration sous-jacente des données observées.
Dans ce travail, la difficulté principale de la structuration est liée à la nature même des relations entre les éléments de l'ensemble étudié. Les concepts classiques de la théorie des espaces métriques et topologiques sont souvent jugés trop exigeants pour modéliser ce type de relations qui sont souvent de nature diverse (distance, dissimilarité, quasipseudométrique, relation binaire, ...).
La prétopologie est un outil qui nous permet de répondre à cette problématique. A partir des relations existant entre les éléments d'un ensemble E, il est possible de construire une application adhérence a(.) sur l'ensemble des parties de la population E et ainsi, de munir E d'une structure prétopologique. Cette adhérence a pour but de définir une certaine notion de proximité entre les parties de E. Sa construction dépend bien évidemment du type de relations existant entre les éléments de E.
Nous avons développé un algorithme de structuration prétopologique appelé algorithme des fermés minimaux. Le principe de cet algorithme consiste à déterminer les plus petits (au sens de l'inclusion) fermés de E, appelés fermés minimaux, puis ceux qui les contiennent jusqu'à obtenir une structuration complète de l'ensemble de la population. Les fermés minimaux correspondent aux groupes homogènes ou interdépendants d'éléments. Les autres fermés correspondent aux relations entre les groupes d'éléments. Il est important de noter que cette méthode de structuration n'est pas une méthode de classification car, on ne construit ni une partition, ni une hiérarchie de la population E (en général, on obtient un recouvrement de E).
Ces travaux ont donné lieu à plusieurs publications et ont été appliqués dans deux études :
-
la première, menée en collaboration avec le laboratoire le Creuset de
Saint-Etienne (programmes CNRS et Avenir - Région Rhône-Alpes), concerne
les externalités géographiques de la recherche française. L'objectif était
de rendre compte des voies de transmission de la connaissance au sein du
territoire français à partir de données représentatives des collaborations
scientifiques (nombre de co-publications entre départements) :
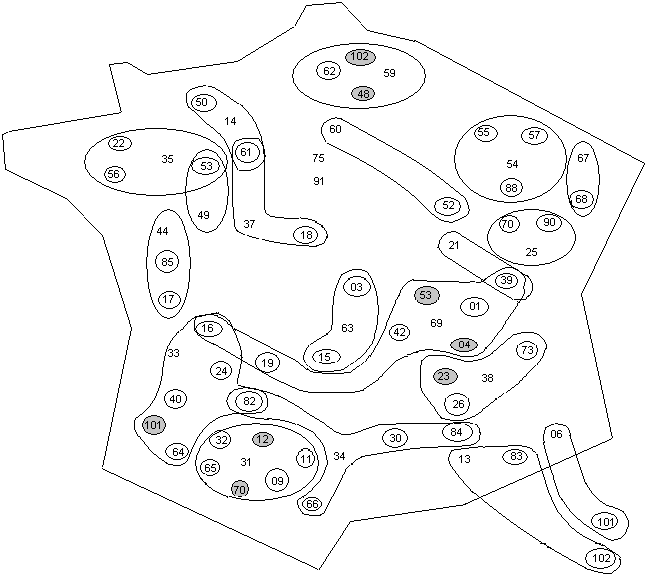
- la deuxième, menée en collaboration avec le Laboratoire d'Economie des Transports de Lyon 2, portait sur les flux de personnes résidants d'une commune et allant travailler dans une autre. L'objectif de cette étude était de mettre en évidence des villes interdépendantes vis-à-vis de ces migrations alternantes.
Modélisation de la dynamique de propagation
D'après la définition d'un espace prétopologique et contrairement aux espaces topologiques, a(a(A)) n'est pas égale à a(A). Ainsi, a(.) n'est pas obligatoirement un fermé de E. Grâce à cette propriété inhérente aux espaces prétopologiques, il est possible d'appliquer plusieurs fois la fonction d'adhérence a(.) sur un ensemble A de manière à modéliser des phénomènes d'extension (dilatation, propagation, influence, ...) des parties de E :
A ⊂ a(A) ⊂ a2(A) ⊂ a3(A) ⊂ a4(A) ⊂ ...
On peut ainsi suivre ou prévoir l'évolution d'une épidémie, étudier un
réseau d'influences, ... .
Ces agrégations successives conduisent, le plus souvent, à l'obtention
de fermés qui vont caractériser des parties homogènes ou interdépendantes
vis-à-vis de la fonction adhérence. Ces fermés peuvent correspondre aux
limites de l'épidémie, du réseau d'influences, ... .
Au delà de cette propriété de l'adhérence, nous avons développé une modélisation dynamique de propagation. Dans le cadre de ce développement, nous nous sommes plus particulièrement intéressés à la dynamique de propagation de la pollution aérienne. Ces travaux sont réalisés dans le cadre du développement de la librairie PretopoLib en collaboration avec l'équipe du LaISC (Laboratoire d'Informatique et des Systèmes Complexes).
Opérateurs prétopologiques de traitement d'images
En traitement d'image également, on s'aperçoit que la prétopologie fournit un cadre mathématique permettant de généraliser certaines approches comme la morphologie mathématique.
J'ai développé une extension des opérateurs de la morphologie mathématique, pour les images à niveaux de gris, grâce à la prétopologie. Ces nouveaux opérateurs utilisent, non pas un élément structurant, mais une base de plusieurs éléments structurants pour la transformation d'images à niveaux de gris. Dans ce travail, j'ai construit deux nouveaux espaces prétopologiques (le premier sur le treillis des images, le second sur Z3) dans lequel je définis les images à niveaux de gris, ainsi que l'ensemble des opérateurs de transformation d'images (les opérateurs de la morphologie mathématique et leurs extensions prétopologiques).
Dans le cadre de la structure sur Z3, je définis une base de famille de voisinages sur tout élément x de Z3 :
∀x ∈ Z3, B(x) = {B1(x), . . . ,Bn(x)}
Chaque élément structurant Bj(x) est un ensemble (volume) de Z3 possédant un point origine, ici en x, faisant partie du volume. A partir de cette base, je construis l'adhérence a(.) :
∀A ⊂ Z3, a(A) = {x ∈ Z3 / ∀Bj(x) ∈ B(x), Bj(x) ∩ A <> ∅}
Cette adhérence permet de créer, sur Z3, une structure prétopologique. Elle généralise la dilatation morphologique (lorsque la base est composée d'un seul élément structurant, cette adhérence correspond à la dilatation morphologique). Il est possible de généraliser l'érosion en définissant l'intérieur (c-duale de l'adhérence), et de redéfinir tous les opérateurs de la morphologie mathématique.
Un des avantages de cette approche prétopologique, au delà du fait qu'on généralise la morphologie mathématique, est qu'on peut, grâce aux formes des éléments de la base structurante, utiliser dans un même opérateur plusieurs éléments structurants et donc mettre en évidence en même temps plusieurs formes dans l'image.
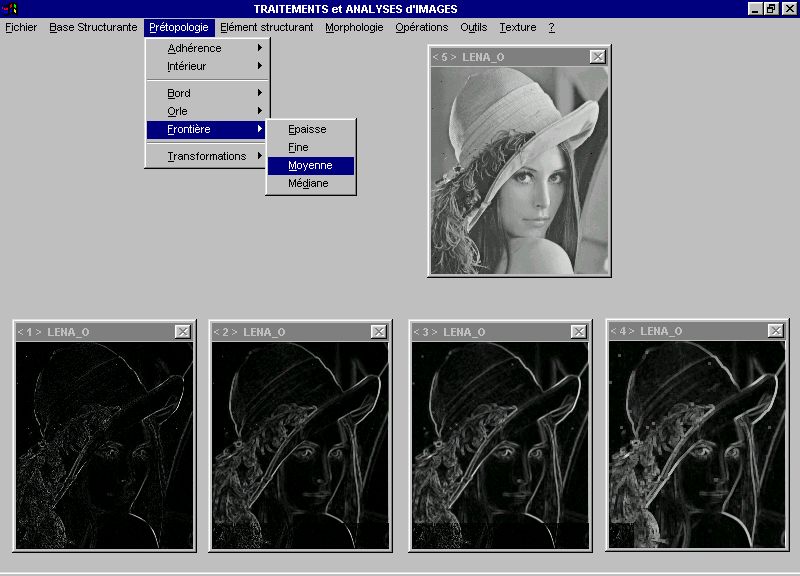
Dans le cadre de ces travaux, j'ai développé une plateforme de traitement d'images implémentant l'ensemble des traitements prétopologiques et morphologiques. Cette plateforme logicielle implémente une structure souple permettant la création de n'importe quelle base structurante destinée aux opérateurs prétopologiques. La figure suivante illustre l'action de l'opérateur frontière sur l'image de Léna (de gauche à droite : frontière fine, médiane, moyenne et épaisse), et ce, avec la base balayant les quatre directions principales :
Publications associées à ce travail
- Basics of Pretopology.
- Pretopological operators for gray-level image analysis.
S.Bonnevay.
Journal : Studia Informatica Universalis, Hermann Editions, vol 7(1), pages 173-195, 2009. - Prétopologie et applications : un état de l'art.
J-P.Auray, S.Bonnevay, M.Bui, G.Duru, M.Lamure.
Journal : Studia Informatica Universalis, Hermann Editions, vol 7(1), pages 27-44, 2009. - A Stochastic and Pretopological Modeling Aerial Pollution of an Urban Area,
S.Ben-Amor, S.Bonnevay, M.Bui, M.Lamure.
Journal : Studia Informatica Universalis, Hermann Editions, vol 7(3), pages 410-426, 2009. - Un modèle prétopologique stochastique pour la simulation de la pollution aérienne.
S.BenAmor, S.Bonnevay, M.Bui, M.Lamure.
Conference : 9th International Conference on System Science in Health Care, Lyon (France), September 2008. - A stochastic and pretopological modeling aerial pollution of an urban area.
M.Lamure, S.Bonnevay, M.Bui, S.Ben-Amor.
Conference : IEEE International Conference on Innvative Internet Community Systems, Schoelcher (Martinique), pages 116-121, June 2008. - Eléments de Prétopologies floues.
M.Egea, S.Bonnevay.
Workshop : Journées d'études Prétopologie et Modélisation, Dinard (France), Mai, 2007. - A pretopological approach for structural analysis.
C.Largeron, S.Bonnevay.
Journal : Information Sciences, vol.144, pages 169-185, July, 2002. - Data analysis based on minimal closed subsets.
- Data analysis based on minimal closed subsets.
S.Bonnevay, C.Largeron,
Conference : International Federation of Classification Societies, Namur (Belgium), july, 2000. - A pretopological approach for structuring data in non-metric spaces.
S.Bonnevay, M.Lamure, C.Largeron, N.Nicoloyannis.
Journal : Electronic Notes in Discrete Mathematics, Melvin F. Janowitz, Vol.2, Elsevier Science Publishers, April, 1999. - Une méthode de structuration par recherche de fermés minimaux - Application à la modélisation de flux de migrations inter-villes.
C.Largeron, S.Bonnevay.
Conference : Société Francophone de Classification, Lyon (France), pages 111-118, Septembre, 1997. - Texture analysis: pretopological approach versus morphology approach.
S.Bonnevay, M.Lamure, N.Nicoloyannis.
Conference : Visual Communications and Image Processing, Taipei (Taiwan), Vol.3, pages 1762-1772, May, 1995.
